Ci sono tanti modi per imparare le disequazioni con valori assoluti… per me il modo migliore è sempre quello di comprendere a fondo tutti i segreti e ragionare sul metodo da seguire, caso per caso.
La prima cosa da comprendere è la definizione di valore assoluto di un numero
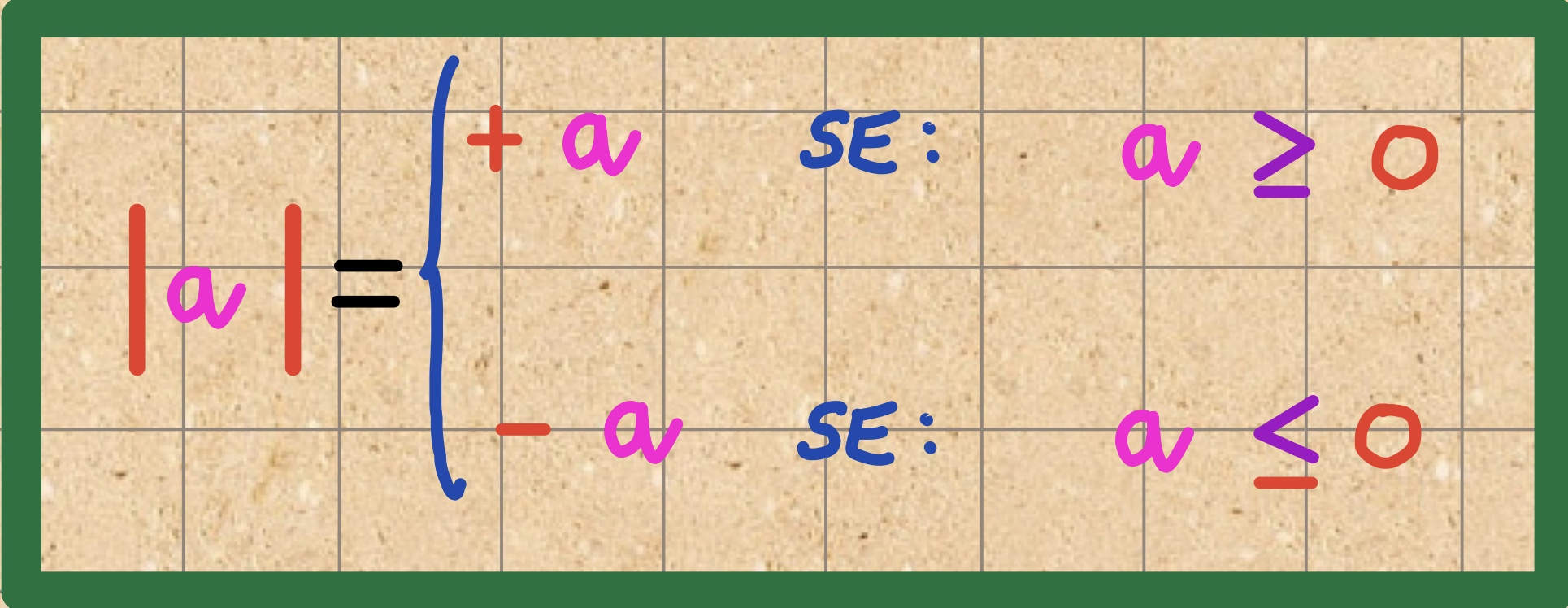
Il valore assoluto è pertanto un “operatore” che assicura la “non negatività” di un numero o di una qualsiasi espressione.. pertanto:

Qualsiasi quantità in valore assoluto è sempre non negativa (ovvero: maggiore o uguale a zero)… pertanto, molti casi semplici di disequazione si possono affrontare meglio ragionando sul significato…
Iniziamo pertanto subito, con la prima unità..
Unità 1: casi semplici
Utilizzando la “non negatività” dei valori assoluti, possiamo subito affrontare il primo caso semplice:

Non impararlo a memoria!!! Ragionare è sempre meglio…
ad esempio, può un valore assoluto essere minore o uguale a zero? si, solo se è zero… e così via…
Ancora più semplice è il secondo caso:

Una quantità in valore assoluto è sempre più grande di un numero non negativo!
Più interessante è il terzo caso, ovvero, quando a “destra” c’è un numero positivo.
Anche in questo caso è più semplice ragionare, pensare ad esempio che i numeri che in valore assoluto “fanno” 3 sono +3 e – 3… quindi “generalizzare” e applicare òa solita logica dei “valori esterni” se il verso è “maggiore”, e “valori interni” se il verso è “minore”:

scarica la lezione completa
File PDF
File PDF2
guarda il video della lezione
Video
Unità 2: caso generale
Nel caso in cui, a “destra” abbiamo una quantità incognita, siamo costretti a studiare due casi, utilizzando la definizione stessa di valore assoluto… anche in questo caso ti consiglio di non imparare a memoria lo schema, ma ragionare sulla sua logica…

scarica la lezione completa
FilePDF
Guarda il video
VIDEO
Unità 3: somma di più valori assoluti
Nel caso in cui in una diseducazione è presente una somma di più valori assoluti, è necessario utilizzare le definizione per individuare attraverso un grafico tutti i casi che si presentano, e risolvere quindi più sistemi:

scarica la lezione completa
File PDF
guarda il video
VIDEO
Attenzione ai casi immediati… dai un’occhiata a queste sfide:
Guarda il video per imparare come risolvere questi esercizi ragionando:
VIDEO

Scarica la lezione completa
File PDF
Guarda il Video
VIDEO
Unità 4:
un valore assoluto dentro l’altro
Un caso più complesso ancora è quello in cui si hanno più valori assoluti, ma questa volta uno dentro l’altro… NO PANIC!!! Basta solo affrontarli uno alla volta, analizzando i casi che si incontrano… ecco qui alcuni esempi di esercizi:

scarica la lezione completa
File PDF
Guarda il video su YouTube
VIDEO
Unità 5:
disequazioni fratte con valore assoluto
A questo punto siamo pronti ad affrontare questioni più articolate: le disequazioni fratte con valori assoluti!! Ma attenzione, in base alla posizione dei valori assoluti, possono essere affrontate in modi differenti.
Ecco alcuni esempi:

scarica la lezione completa
File PDF
Guarda il video su YouTube
VIDEO
